Sparse ruler
A sparse ruler is a ruler in which some of the distance marks are missing, yet which allows you to measure any integer distance up to its full length. More abstractly, a sparse ruler of length  with
with  marks is a sequence of integers
marks is a sequence of integers 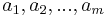 where
where 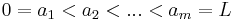 . The marks
. The marks 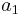 and
and 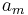 correspond to the ends of the ruler. In order to measure the distance
correspond to the ends of the ruler. In order to measure the distance  , with
, with 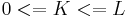 there must be marks
there must be marks 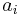 and
and 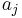 such that
such that 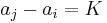 .
.
A sparse ruler is called minimal if there is no sparse ruler of length  with
with 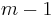 marks. In other words, if any of the marks is removed one can no longer measure all of the distances. A sparse ruler is called maximal if there is no sparse ruler of length
marks. In other words, if any of the marks is removed one can no longer measure all of the distances. A sparse ruler is called maximal if there is no sparse ruler of length 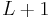 with
with  marks. A sparse ruler is called optimal if it is both minimal and maximal.
marks. A sparse ruler is called optimal if it is both minimal and maximal.
Since the number of distinct pairs of marks is 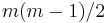 , this is an upper bound on the length
, this is an upper bound on the length  of any maximal sparse ruler with
of any maximal sparse ruler with  marks. This upper bound can be achieved only for 2, 3 or 4 marks. For larger numbers of marks, the difference between the optimal length and the bound grows gradually, and unevenly.
marks. This upper bound can be achieved only for 2, 3 or 4 marks. For larger numbers of marks, the difference between the optimal length and the bound grows gradually, and unevenly.
For example, for 6 marks the upper bound is 15, but the maximal length is 13. There are 3 different configurations of sparse rulers of length 13 with 6 marks. One is {0, 1, 2, 6, 10, 13}. To measure a length of 7, say, with this ruler you would take the distance between the marks at 6 and 13.
Sparse rulers are closely related to, but different from Golomb rulers because Golomb rulers require that all of the differences 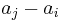 be distinct. In general, a Golomb ruler with
be distinct. In general, a Golomb ruler with  marks will be considerably longer than an optimal sparse ruler with
marks will be considerably longer than an optimal sparse ruler with  marks, since
marks, since 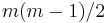 is a lower bound for the length of a Golomb ruler. A long Golomb ruler will have gaps, that is, it will have distances which it cannot measure. For example, the optimal Golomb ruler {0, 1, 4, 10, 12, 17} has length 17, but cannot measure lengths of 14 or 15.
is a lower bound for the length of a Golomb ruler. A long Golomb ruler will have gaps, that is, it will have distances which it cannot measure. For example, the optimal Golomb ruler {0, 1, 4, 10, 12, 17} has length 17, but cannot measure lengths of 14 or 15.
Wichmann rulers
Many optimal rulers are of the form W(r,s) = 1^r, r+1, (2r+1)^r, (4r+3)^s, (2r+2)^(r+1), 1^r, where a^b represents b segments of length a. Thus, if r = 1 and s = 2, then W(1,2) has (in order):
1 segment of length 1,
1 segment of length 2,
1 segment of length 3,
2 segments of length 7,
2 segments of length 4,
1 segment of length 1
That gives the ruler {0, 1, 3, 6, 13, 20, 24, 28, 29}. The length of a Wichmann ruler is 4r(r+s+2)+3(s+1) and the number of marks is 4r+s+3. Note that not all Wichmann rulers are optimal and not all optimal rulers can be generated this way. None of the optimal rulers of length 1, 13, 17, 23 and 58 follow this pattern, but no optimal rulers with length greater than 68 are known that are not Wichmann rulers.
Examples
The following are examples of minimal sparse rulers. Optimal rulers are highlighted. When there are too many to list, not all are included. Mirror images are not shown.
| Length | Marks | Number | Examples | List Form | Wichmann |
|---|---|---|---|---|---|
| 1 | 2 | 1 | II | {0, 1} | |
| 2 | 3 | 1 | III | {0, 1, 2} | |
| 3 | 3 | 1 | II.I | {0, 1, 3} | W(0,0) |
| 4 | 4 | 2 | III.I II.II |
{0, 1, 2, 4} {0, 1, 3, 4} |
|
| 5 | 4 | 2 | III..I II.I.I |
{0, 1, 2, 5} {0, 1, 3, 5} |
|
| 6 | 4 | 1 | II..I.I | {0, 1, 4, 6} | W(0,1) |
| 7 | 5 | 6 | IIII...I III.I..I III..I.I II.I.I.I II.I..II II..II.I |
{0, 1, 2, 3, 7} {0, 1, 2, 4, 7} {0, 1, 2, 5, 7} {0, 1, 3, 5, 7} {0, 1, 3, 6, 7} {0, 1, 4, 5, 7} |
|
| 8 | 5 | 4 | III..I..I II.I...II II..I.I.I II...II.I |
{0, 1, 2, 5, 8} {0, 1, 3, 7, 8} {0, 1, 4, 6, 8} {0, 1, 5, 6, 8} |
|
| 9 | 5 | 2 | III...I..I II..I..I.I |
{0, 1, 2, 6, 9} {0, 1, 4, 7, 9} |
- W(0,2) |
| 10 | 6 | 19 | IIII..I...I | {0, 1, 2, 3, 6, 10} | |
| 11 | 6 | 15 | IIII...I...I | {0, 1, 2, 3, 7, 11} | |
| 12 | 6 | 7 | IIII....I...I III...I..I..I II.I.I.....II II.I...I...II II..II....I.I II..I..I..I.I II.....II.I.I |
{0, 1, 2, 3, 8, 12} {0, 1, 2, 6, 9, 12} {0, 1, 3, 5, 11, 12} {0, 1, 3, 7, 11, 12} {0, 1, 4, 5, 10, 12} {0, 1, 4, 7, 10, 12} {0, 1, 7, 8, 10, 12} |
- - - - - W(0,3) - |
| 13 | 6 | 3 | III...I...I..I II..II.....I.I II....I..I.I.I |
{0, 1, 2, 6, 10, 13} {0, 1, 4, 5, 11, 13} {0, 1, 6, 9, 11, 13} |
|
| 14 | 7 | 65 | IIIII....I....I | {0, 1, 2, 3, 4, 9, 14} | |
| 15 | 7 | 40 | II.I..I...I...II II..I..I..I..I.I |
{0, 1, 3, 6, 10, 14, 15} {0, 1, 4, 7, 10, 13, 15} |
W(1,0) W(0,4) |
| 16 | 7 | 16 | IIII....I...I...I | {0, 1, 2, 3, 8, 12, 16} | |
| 17 | 7 | 6 | IIII....I....I...I III...I...I...I..I III.....I...I.I..I III.....I...I..I.I II..I.....I.I..I.I II......I..I.I.I.I |
{0, 1, 2, 3, 8, 13, 17} {0, 1, 2, 6, 10, 14, 17} {0, 1, 2, 8, 12, 14, 17} {0, 1, 2, 8, 12, 15, 17} {0, 1, 4, 10, 12, 15, 17} {0, 1, 8, 11, 13, 15, 17} |
|
| 18 | 8 | 250 | II..I..I..I..I..I.I | {0, 1, 4, 7, 10, 13, 16, 18} | W(0,5) |
| 19 | 8 | 163 | IIIII....I....I....I | {0, 1, 2, 3, 4, 9, 14, 19} | |
| 20 | 8 | 75 | IIIII.....I....I....I | {0, 1, 2, 3, 4, 10, 15, 20} | |
| 21 | 8 | 33 | IIIII.....I.....I....I | {0, 1, 2, 3, 4, 10, 16, 21} | |
| 22 | 8 | 9 | IIII....I....I....I...I III.......I....I..I..II II.I.I........II.....II II.I..I......I...I...II II.I.....I.....I...II.I II..II......I.I.....I.I II....II..I.......I.I.I II....I..I......I.I.I.I II.....II........II.I.I |
{0, 1, 2, 3, 8, 13, 18, 22} {0, 1, 2, 10, 15, 18, 21, 22} {0, 1, 3, 5, 14, 15, 21, 22} {0, 1, 3, 6, 13, 17, 21, 22} {0, 1, 3, 9, 15, 19, 20, 22} {0, 1, 4, 5, 12, 14, 20, 22} {0, 1, 6, 7, 10, 18, 20, 22} {0, 1, 6, 9, 16, 18, 20, 22} {0, 1, 7, 8, 17, 18, 20, 22} |
- - - W(1,1) - - - - - |
| 23 | 8 | 2 | III........I...I..I..I.I II..I.....I.....I.I..I.I |
{0, 1, 2, 11, 15, 18, 21, 23} {0, 1, 4, 10, 16, 18, 21, 23} |
|
| 24 | 9 | 472 | IIIIII......I.....I.....I | {0, 1, 2, 3, 4, 5, 12, 18, 24} | |
| 25 | 9 | 230 | IIIIII......I......I.....I | {0, 1, 2, 3, 4, 5, 12, 19, 25} | |
| 26 | 9 | 83 | IIIII.....I....I.....I....I | {0, 1, 2, 3, 4, 10, 15, 21, 26} | |
| 27 | 9 | 28 | IIIII.....I.....I.....I....I | {0, 1, 2, 3, 4, 10, 16, 22, 27} | |
| 28 | 9 | 6 | III..........I....I..I..I..II II.I.I.I..........II.......II II.I..I..I......I......I...II II.I.....I.....I.....I...II.I II.....I...I........I..I.II.I II.......II..........II.I.I.I |
{0, 1, 2, 13, 18, 21, 24, 27, 28} {0, 1, 3, 5, 7, 18, 19, 27, 28} {0, 1, 3, 6, 9, 16, 23, 27, 28} {0, 1, 3, 9, 15, 21, 25, 26, 28} {0, 1, 7, 11, 20, 23, 25, 26, 28} {0, 1, 9, 10, 21, 22, 24, 26, 28} |
|
| 29 | 9 | 3 | III...........I...I..I..I..I.I II.I..I......I......I...I...II II..I.....I.....I.....I.I..I.I |
{0, 1, 2, 14, 18, 21, 24, 27, 29} {0, 1, 3, 6, 13, 20, 24, 28, 29} {0, 1, 4, 10, 16, 22, 24, 27, 29} |
- W(1,2) - |
| 35 | 10 | 5 | III..............I...I..I..I..I..I.I II.I..I..I......I......I......I...II II.I..I..I.........I...I......I...II II..II..........I.I......I.I.....I.I II..I.....I.....I.....I.....I.I..I.I |
{0, 1, 2, 17, 21, 24, 27, 30, 33, 35} {0, 1, 3, 6, 9, 16, 23, 30, 34, 35} {0, 1, 3, 6, 9, 19, 23, 30, 34, 35} {0, 1, 4, 5, 16, 18, 25, 27, 33, 35} {0, 1, 4, 10, 16, 22, 28, 30, 33, 35} |
|
| 36 | 10 | 1 | II.I..I......I......I......I...I...II | {0, 1, 3, 6, 13, 20, 27, 31, 35, 36} | W(1,3) |
| 43 | 11 | 1 | II.I..I......I......I......I......I...I...II | {0, 1, 3, 6, 13, 20, 27, 34, 38, 42, 43} | W(1,4) |
| 46 | 12 | 342 | III..I....I....I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 32, 38, 44, 45, 46} | W(2,1) |
| 50 | 12 | 2 | IIII...................I....I...I...I...I...I..I..I II.I..I.....I......I......I......I......I...I...II |
{0, 1, 2, 3, 23, 28, 32, 36, 40, 44, 47, 50} {0, 1, 3, 6, 13, 20, 27, 34, 41, 45, 49, 50} |
- W(1,5) |
| 57 | 13 | 12 | III..I....I....I..........I..........I.....I.....I.....III II.I..I......I......I......I......I......I......I...I...II |
{0, 1, 2, 5, 10, 15, 26, 37, 43, 49, 55, 56, 57} {0, 1, 3, 6, 13, 20, 27, 34, 41, 48, 52, 56, 57} |
W(2,2) W(1,6) |
| 58 | 13 | 6 | IIII.......................I....I...I...I...I...I...I..I..I III...I.I........I........I........I........I..I......I..II III.....I......II.........I.........I.........I..I...I.I..I II.I..I..........I..I......I.......I.........I...I...I...II II.I..I..........I......I..I..........I......I...I...I...II II...I..I...I........I........I........I........I....II.I.I |
{0, 1, 2, 3, 27, 32, 36, 40, 44, 48, 52, 55, 58} {0, 1, 2, 6, 8, 17, 26, 35, 44, 47, 54, 57, 58} {0, 1, 2, 8, 15, 16, 26, 36, 46, 49, 53, 55, 58} {0, 1, 3, 6, 17, 20, 27, 35, 45, 49, 53, 57, 58} {0, 1, 3, 6, 17, 24, 27, 38, 45, 49, 53, 57, 58} {0, 1, 5, 8, 12, 21, 30, 39, 48, 53, 54, 56, 58} |
|
| 68 | 14 | 2 | III..I....I....I..........I..........I..........I.....I.....I.....III III.....I......II.........I.........I.........I.........I..I...I.I..I |
{0, 1, 2, 5, 10, 15, 26, 37, 48, 54, 60, 66, 67, 68} {0, 1, 2, 8, 15, 16, 26, 36, 46, 56, 59, 63, 65, 68} |
W(2,3) - |
| 79 | 15 | 1 | III..I....I....I..........I..........I..........I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 37, 48, 59, 65, 71, 77, 78, 79} | W(2,4) |
| 90 | 16 | 1 | III..I....I....I..........I..........I..........I..........I..........I.....I.....I.....III | {0, 1, 2, 5, 10, 15, 26, 37, 48, 59, 70, 76, 82, 88, 89, 90} | W(2,5) |
| 101 | 17 | 1 | III..I....I....I..........I..........I..........I..........I..........I..........I.....I.....I.....III | {0,1,2,5,10,15,26,37,48,59,70,81,87,93,99,100,101} | W(2,6) |
| 112 | 18 | 1 | {0,1,2,5,10,15,26,37,48,59,70,81,92,98,104,110,111,112} | W(2,7) | |
| 123 | 19 | 2 | {0,1,2,3,7,14,21,28,43,58,73,88,96,104,112,120,121,122,123} {0,1,2,5,10,15,26,37,48,59,70,81,92,103,109,115,121,122,123} |
W(3,4) W(2,8) |
|
| 138 | 20 | 1 | {0,1,2,3,7,14,21,28,43,58,73,88,103,111,119,127,135,136,137,138} | W(3,5) |